UnityやBlenderのように手軽に3DCGを体験できるソフトが増えてきたものの、実際にはどのような原理でコンピューターグラフィックスが作られているのかを理解している人はそれほど多くないように思います。わたしも完全に理解しているとは言い難かったのですが、今回グラフィックスを改めて勉強しなおす機会に恵まれたので、その備忘録として本記事を書き残すことにしました。
こちらの記事は、サイバーエージェントさんが主催するGraphicsAcademy【一日目】に参加したときの講座内容を元に執筆しています。サイバーエージェントGraphicsAcademyについては、こちらをご覧ください。
Contents
メッシュの基礎知識
まず最初は、メッシュについて基本構成をおさらいします。メッシュとは、3D空間における物の形状を定義したデータです。ゲーム制作だとfbxが一般的ですが、ほかにもいくつか形式があります。ただ、どんな拡張子であれ、メッシュを構成する基本的な要素はほとんど変わりません。メッシュを構成する要素としては、
- 頂点(vertex)
- 法線(normal)
- テクスチャ座標(UV)
- 頂点カラー(color)
- ポリゴンの構成頂点リスト(index)
といったものがあります。なかでも、vertexとindexは重要です。この二つはポリゴン描画に必須なため、これらがないと面を描画することができません。
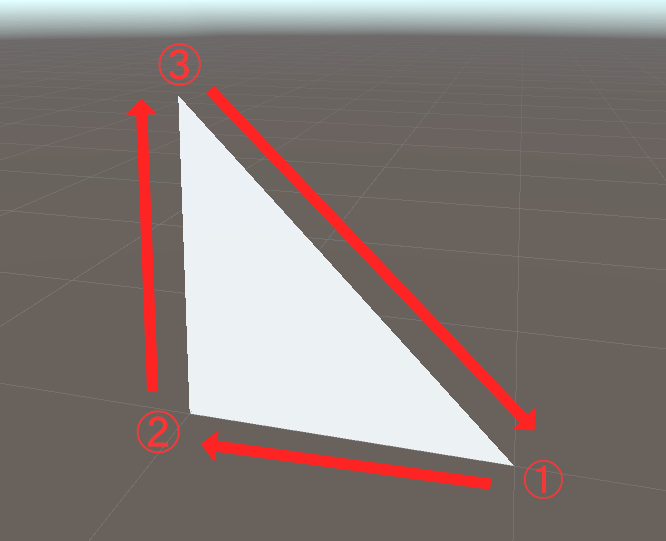
最低限この二つがわかればメッシュを表示することができるのですが、頂点の組み合わせに関しては、順番が重要です。なぜなら、頂点を時計回りに結んだ面が表として定義されているためです。裏となる面は通常描画されません。(※シェーダーによっては裏面を描画するものもあります)
また、このほかにもメッシュデータはアニメーションといったデータを含むこともあります。ただし、そういったデータをスクリプトのみで作ることはかなり難しいので、DCC(Degital Contents Creation: BlenderとかMayaといったソフトのこと)でモデリングしましょう。
Unityでポリゴンを描画してみる
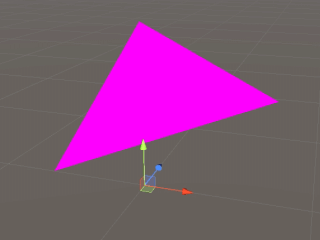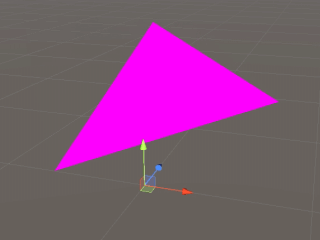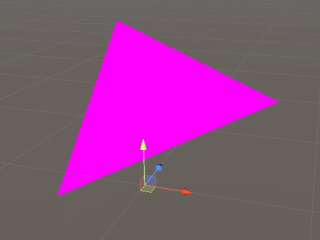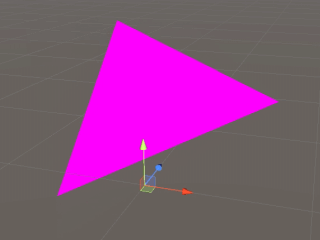
さて、メッシュの基本仕様がおさらいしたところで、Unityを使ってどのようにポリゴンを作るのかを確認してみます。Unityでポリゴン一枚を描画するコードは以下の通りです。ここではポリゴン一枚を描画しています。
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
[ExecuteInEditMode]
public class TriangleGenerator : MonoBehaviour
{
private MeshFilter _meshFilter;
[SerializeField] private Vector3 vertex1 = new Vector3(0.0f, 0.0f, 0.0f);
[SerializeField] private Vector3 vertex2 = new Vector3(1.0f, 0.0f, 0.0f);
[SerializeField] private Vector3 vertex3 = new Vector3(1.0f, 1.0f, 0.0f);
private void Start()
{
_meshFilter = GetComponent<MeshFilter>();
CreatePolygon();
}
private void OnValidate()
{
CreatePolygon(); //vertex1~3の値が変更されたときにポリゴンを作り直す
}
public void CreatePolygon()
{
List<Vector3> vertices = new List<Vector3>() {
vertex1,
vertex2,
vertex3
};
List<int> triangles = new List<int> {
0, 1, 2
};
Mesh mesh = new Mesh(); // メッシュを作成
mesh.Clear(); // メッシュ初期化
mesh.SetVertices(vertices); // メッシュに頂点を登録する
mesh.SetTriangles(triangles, 0); // メッシュにインデックスリストを登録する
mesh.SetIndices(triangles, MeshTopology.Triangles, 0); //MeshTopologyを変更すればラインや点群といった表示もできる
mesh.RecalculateNormals(); // 法線の再計算
mesh.name = "SimplePolygon";
_meshFilter.mesh = mesh;
}
}描画工程について
簡単なポリゴンを作ることはできましたが、実際にはそれがどうように解釈されて、どのようにディスプレイに描画されているのかを考えてみます。さきほど説明した通り、メッシュはあくまで数字を記録したリストにすぎません。ここからディスプレイに形や色を表示するにはさまざまな工程が絡んできます。
大まかな工程を先に示してしまうと、
- 頂点の座標変換(※)
- 頂点のシェーディング
- ポリゴンのラスタライズ
- ディスプレイに表示
※ M:モデリング座標変換 ⇒ V:視野変換 ⇒ P:投影変換 ⇒ U:ビューポート変換
となっています。すべての工程を一度に理解するのは、なかなか難しいので、まずは1の「頂点の座標変換」について詳しく解説していきます。
なぜこの座標変換が必要なのかというと、メッシュが持つ頂点はすべてワールド座標を基準としていますが、ディスプレイに表示するにはこれらが二次元座標に置き換わる必要があるためです。
たとえば三次元空間上に適当な座標点Aがあったとして、それをカメラが捉えたとき、その点Aがディスプレイのどこか(x, y)に表示されます。このxとyを、点Aを使った行列計算によって求めることを、「頂点の座標変換」といいます。
各座標系について
ワールド座標からディスプレイ座標への変換は、残念ながら一発で求めることはできません。数回の行列計算が必要になります。この時に、どの座標に変換されたのかをしっかりと理解しておかないと、非常に混乱しやすいです。ここではそれぞれの変換工程をひとつづつ切り分けて解説していきます。
モデリング座標変換
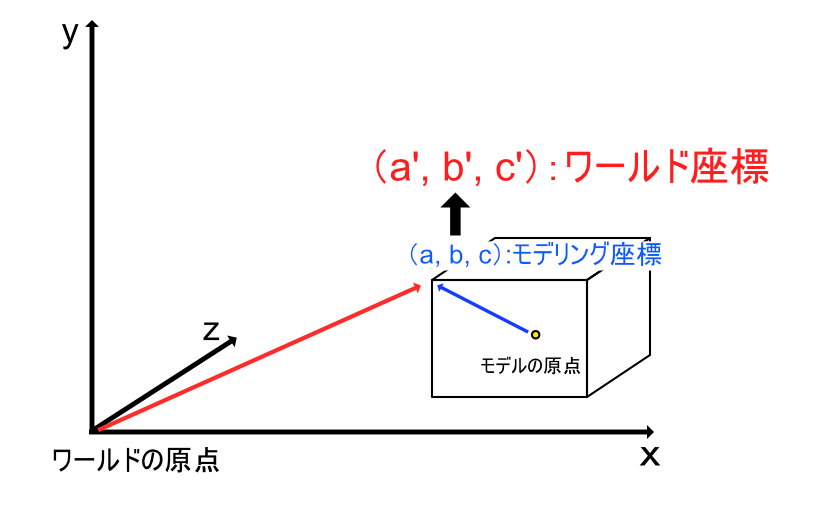
モデリング座標変換とは、モデリング座標系からワールド座標系に変換する工程のことです。モデリング座標は各モデルの原点から見た座標空間になっているので、これをワールドの原点を基準とした座標空間に変換することが必要になります。モデリング座標の頭文字をとり、MVPU変換のMに相当します。
視野変換
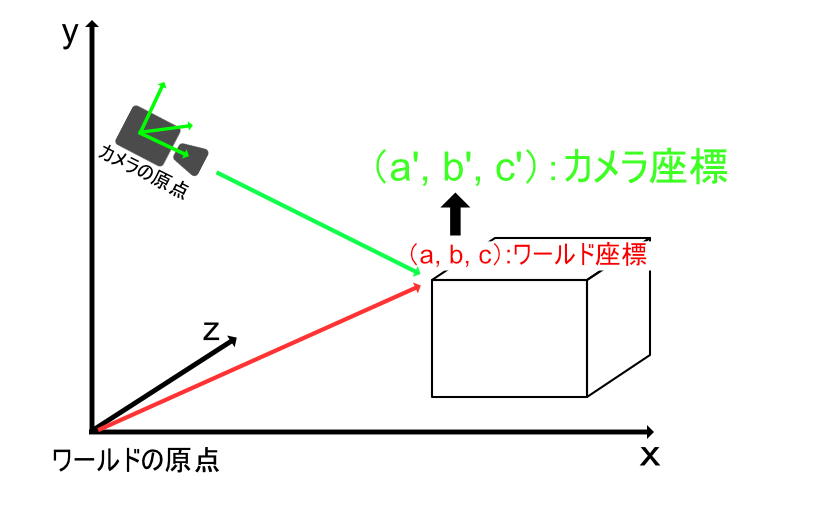
視野変換は、ワールド座標系からカメラ座標系に変換する工程のことです。先ほどワールドに変換した座標系を今度はカメラを基準とした座標系に変換します。Viewingの頭文字をとり、MVPU変換のVに相当します。
投影変換
投影変換は、カメラ座標系を投影座標系に変換する工程のことです。この工程で、これまで3D空間で扱っていたものが2D空間に圧縮されます。正確にはz値(奥行)を持つため、完全な二次元空間ではありませんが、イメージとしては空間から平面に変換されたといっても過言ではありません。Projectionの頭文字をとり、MVPU変換のPに相当します。
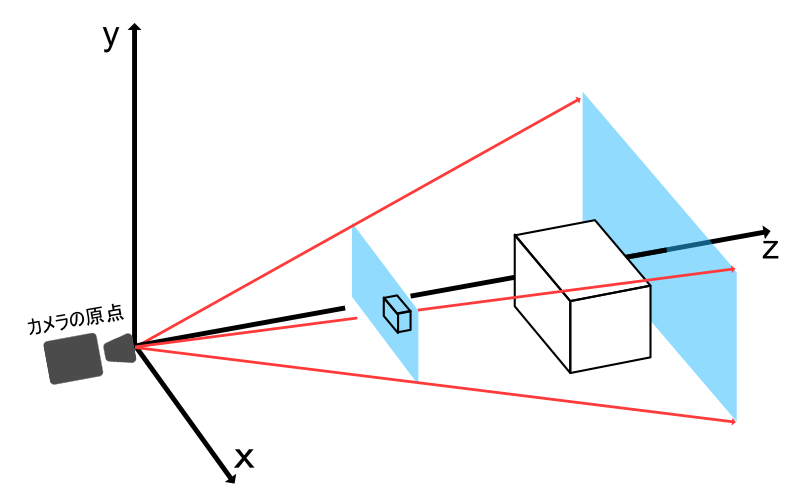
ここでいう投影座標系には、透視投影と平行投影の二つがあります。Unityのカメラでいうところの「Perspective」と「Orthographic」です。

こちらの記事(https://light11.hatenadiary.com/entry/2018/06/10/233954)を参考にプロジェクション座標変換を視覚化してみます。カメラのフラスタムがProjection座標に変換される過程が、以下のイメージからわかると思います。
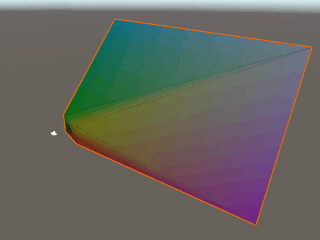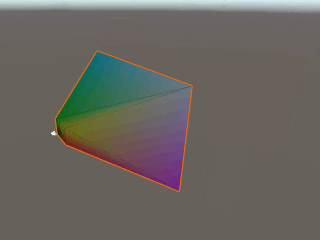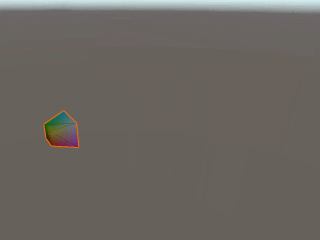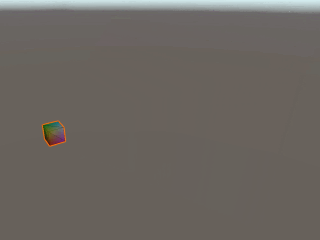
重要なポイントは、カメラが映す奥行が0~1の距離に正規化されている点です。この正規化された奥行は、z値として利用され、主にオブジェクトの前後関係を判定します。また、このz値の0~1は線形ではないことに注意してください。カメラに近いほどz値の精度が高くなった方が都合がいい場合が多いため、指数的な傾斜がかかっています。
加えて、このz値はプラットフォームやUnityのバージョンによっては異なることも気をつけてください。1がnear、0がfarとして定義されている場合があります。
ビューポート変換
ビューポート変換は、投影座標系をデバイス座標系に変換する工程のことです。この工程で、デバイスのディスプレイが表示できる範囲だけが切り取られ、ディスプレイに画像として表示されることになります。Viewportの頭文字をとり、MVPU変換のVに相当…と言いたいところですが、視野変換(viewing)ですでにVを使用しているので、U(似てるから?)が当てられています。
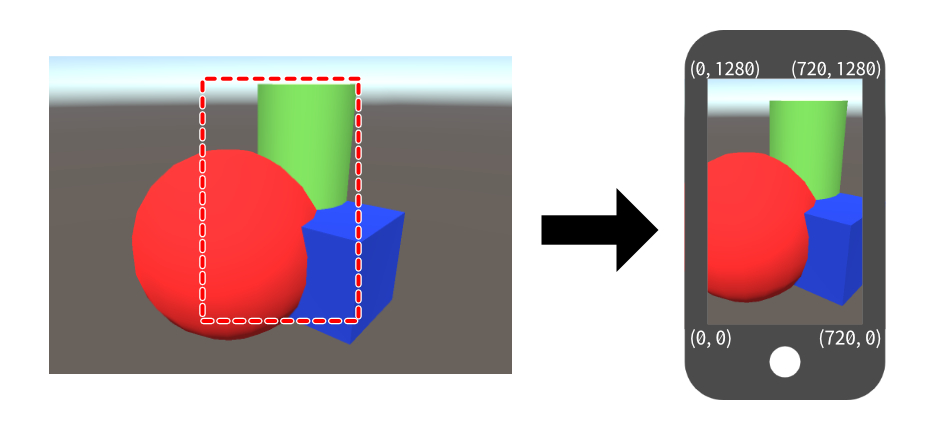
そして、これらの行程を数式としてあらわすと、モデリング座標系点vとした場合、ディスプレイ座標点v’は、
$v’ = UPVMv$
という行列乗算によって求められる、ということになります。
行列計算とその利点
ここまで座標変換について解説してきました。おおよそのイメージがつかめたと思いますが、次は実際の数値を入れて計算をする方法を見ていきましょう。
こうした座標系の変換には行列を使います。行列とは、縦と横に数字や式を並べた配列です。なぜわざわざ行列を使うのかというと、平行移動のみ加算で扱いにくいので、次元をあげることですべて乗算に持ち込むことができるためです。
通常座標
平行移動 $\begin{pmatrix} x’ \\ y’ \\ \end{pmatrix} = \begin{pmatrix} x \\ y \\ \end{pmatrix} + \begin{pmatrix} t_{x} \\ t_{y} \\ \end{pmatrix}$
拡大縮小 $\begin{pmatrix} x’ \\ y’ \\ \end{pmatrix} = \begin{pmatrix} s_{x} & 0 \\ 0 & s_{y} \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix}$
回転 $\begin{pmatrix} x’ \\ y’ \\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix}$
同時座標
平行移動 $\begin{pmatrix} x’ \\ y’ \\ 1\\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\\ \end{pmatrix}$
拡大縮小 $\begin{pmatrix} x’ \\ y’ \\ 1\\ \end{pmatrix} = \begin{pmatrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\\ \end{pmatrix}$
回転 $\begin{pmatrix} x’ \\ y’ \\ 1\\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1\\ \end{pmatrix}$
なお、行列の乗算は、順番を入れ替えると意味が変わってしまうので注意が必要です。移動、回転、拡大の他にも、
- 鏡面
- せん断
といった操作も行列計算で表すことができます。こうした行列変換に関する解説はネットにたくさんの記事が公開されていますので、詳しい計算過程を勉強したい方はぜひそちらを探してみてください。
演習問題
ここまで学んだことを参考に以下の演習問題に挑戦してみてください。
①スクリプトからCubeを作成してみる。
②スクリプトからSphereを作成してみる。
③モデリング座標Aをカメラ標系に変換するスクリプトを作成してみる。
解説
①Cubeの作成
頂点数24にしてCubeのノーマルがsmoothにならないように調整します。ポイントとしては、エッジを立てる辺は頂点を重ねて置く、という点です。サンプルコードでは、下の画像の中で、真ん中にあるキューブを生成してます。

using System.Collections.Generic;
using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
[ExecuteInEditMode]
public class FlatCubeGenerator : MonoBehaviour
{
private Mesh _mesh;
private MeshFilter _meshFilter;
private void Start()
{
_mesh = GetComponent<Mesh>();
_meshFilter = GetComponent<MeshFilter>();
CreateFlatCube();
}
void CreateFlatCube()
{
List<Vector3> vertices = new List<Vector3>() {
// 0
new Vector3(0.0f, 0.0f, 0.0f), // 正面
new Vector3(1.0f, 0.0f, 0.0f),
new Vector3(1.0f, 1.0f, 0.0f),
new Vector3(0.0f, 1.0f, 0.0f),
// 4
new Vector3(1.0f, 1.0f, 0.0f), // 上面
new Vector3(0.0f, 1.0f, 0.0f),
new Vector3(0.0f, 1.0f, 1.0f),
new Vector3(1.0f, 1.0f, 1.0f),
// 8
new Vector3(1.0f, 0.0f, 0.0f), // 右面
new Vector3(1.0f, 1.0f, 0.0f),
new Vector3(1.0f, 1.0f, 1.0f),
new Vector3(1.0f, 0.0f, 1.0f),
// 12
new Vector3(0.0f, 0.0f, 0.0f), // 左面
new Vector3(0.0f, 1.0f, 0.0f),
new Vector3(0.0f, 1.0f, 1.0f),
new Vector3(0.0f, 0.0f, 1.0f),
// 16
new Vector3(0.0f, 1.0f, 1.0f), // 背面
new Vector3(1.0f, 1.0f, 1.0f),
new Vector3(1.0f, 0.0f, 1.0f),
new Vector3(0.0f, 0.0f, 1.0f),
// 20
new Vector3(0.0f, 0.0f, 0.0f), // 下面
new Vector3(1.0f, 0.0f, 0.0f),
new Vector3(1.0f, 0.0f, 1.0f),
new Vector3(0.0f, 0.0f, 1.0f),
};
List<int> triangles = new List<int> {
0, 3, 2, 0, 2, 1, //前面 ( 0 - 3)
5, 6, 7, 5, 7, 4, //上面 ( 4 - 7)
8, 9,10, 8,10,11, //右面 ( 8 - 11)
15,14,13, 15,13,12, //左面 (12 - 15)
16,18,17, 16,19,18, //奥面 (16 - 19)
23,20,21, 23,21,22, //下面 (20 - 23)
};
Mesh mesh = new Mesh(); // メッシュを作成
mesh.Clear(); // メッシュ初期化
mesh.SetVertices(vertices); // メッシュに頂点を登録する
mesh.SetTriangles(triangles, 0); // メッシュにインデックスリストを登録する
mesh.RecalculateNormals(); // 法線の再計算
_meshFilter.mesh = mesh;
}
}
②Sphereの作成
何気なくプリミティブで呼び出せてしまうゆえに、コードにしてみると結構説明しにくい部分が多いかもしれません。詳しい解説は長くなりすぎるので、別記事にします。
③カメラ座標系の確認
自分自身で適当な座標を入れて変換を確認する場合は、カメラを上下移動させるだけではなく、回転も加えたほうがいいです。回転成分がないと、一見して計算結果が変わっていないように見える場合があるためです。
public class MatrixConvertProcessWatcher : MonoBehaviour
{
private void Start()
{
ConvertMatrix();
}
[ContextMenu("Convert!")]
public void ConvertMatrix()
{
var camera = FindObjectOfType<Camera>();
var modelMatrix = transform.localToWorldMatrix; //オブジェクトのモデリング座標マトリックス
Debug.Log("modelMatrix: \n" + modelMatrix);
var vertex = new Vector4(1, 2, 3, 1); //適当な頂点座標を用意
Debug.Log(modelMatrix * vertex); //モデリング座標と用意した頂点で行列変換し、頂点をワールド座標に変換
var viewMatrix = camera.worldToCameraMatrix; //カメラの座標マトリックス
Debug.Log("viewMatrix: \n" + viewMatrix);
var viewport = viewMatrix * modelMatrix; //カメラとモデリングの座標マトリックスから投影変換
Debug.Log("viewport: \n" + viewport);
var targetPos = viewport * vertex; //最終的なディスプレイ座標
targetPos.z *= -1; //z値を反転
Debug.Log(targetPos);
}
}まとめ
CGの基礎原理について学習しましたが、かなり数学的な要素が強く苦労すると思います。とくに行列計算は普段あまりなじみがないことでしょう。とはいっても実際に数値を計算することはほとんどないので、Unityが提供するメソッドやフィールドを使いこなせば、導出はそれほどむずかしくないはずです。